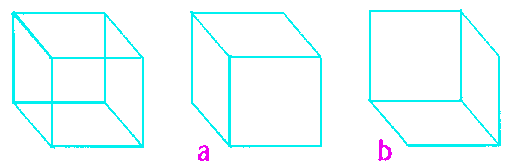
Les capacités de calcul des premiers micro-ordinateurs ne permettaient de donner l’illusion d’une troisième dimension qu’à des objets de forme simple. La technique retenue était celle de la perspective dite "fil de fer", où seules les arêtes de l’objet étaient rendues visibles. Mais dans ce cas, la perception de l'objet est douteuse (un cube représenté en perspective fil de fer peut être perçu de deux façons : face vers le bas (a) ou face vers le haut (b)).

Autre inconvénient : comme le cerveau humain n’a pas de repère de profondeur, il n’arrive pas à reconstituer clairement la troisième dimension de l’objet.
On a donc rapidement ressenti le besoin d’affiner la représentation des images
: il faut, pour cela, maîtriser des techniques d’élimination des faces cachées dont le principe est
élémentaire. Connaissant la position de l’observateur, il s’agit de trouver
quelles facettes de la figure sont les plus proches de lui, les autres étant considérées
comme totalement ou partiellement masquées. Principe simple, mais assez difficile a appliquer
dès que l’objet devient complexe. De nombreux algorithmes ont donc été étudiés, parmi lesquels celui du
"lancer ou suivi de rayon" proposé, à l’origine, comme un moyen simple d’éliminer les
faces cachées. Sur le plan technique, il présente quelques défauts, mais permet
d’obtenir des images remarquablement réalistes.

En fait, la plupart des algorithmes reposent sur l’idée qu’un observateur perçoit une scène uniquement parce qu’il y a une ou plusieurs sources de lumière pour l’éclairer. Les calculs sont donc logiquement effectués en considérant les rayons envoyés par la source lumineuse. On examine leurs comportements successifs pour savoir si, en fin de compte, ils seront ou non perçus par l’œil de l’observateur. L’image de l’objet est reconstituée, conforme à la réalité.
Cette méthode, sur le plan du calcul, conduit à un certain gaspillage car, pour chaque point de l’objet représenté sur l’écran, seul le rayon qui part de la source lumineuse et qui parvient à l’oeil de l’observateur est utile. D’où l’idée géniale du suivi de rayon, qui consiste à prendre le problème à l’envers, c’est-à-dire partir de l’oeil de l’observateur, et non de la source de lumière, pour ne considérer que les rayons utiles. On imagine ainsi le rayon qui part de l’oeil de l’observateur, et on trace une droite reliant cet oeil à un point de l’écran, ou plus exactement à un point de l’image virtuelle dont on cherche la représentation. Sur l’écran, chaque point est défini par sa couleur et son intensité lumineuse. Pour les calculer, il suffit d’imaginer que l’objet réel et les sources lumineuses qui l’éclairent existent derrière l’écran. On prolonge alors notre droite (le rayon primaire) au-delà de l’écran pour savoir quel est le premier élément de l’objet rencontré. Supposons pour simplifier que cet élément soit opaque et réfléchissant. On calcule la déviation du rayon sur l’objet et on cherche à savoir s’il atteint une source lumineuse. Si oui, on sait que le trajet inverse de la lumière sera le même et, connaissant les caractéristiques de la source lumineuse (intensité) et celles de la surface de l’objet, on peut déterminer les valeurs d’intensité et de couleur du point correspondant sur l’écran. Si la surface n’est pas réfléchissante, il faut envoyer, vers les différentes sources lumineuses, des rayons secondaires à partir du point d’intersection du rayon primaire avec l’objet. L’éclairement du point en question dépendra de la contribution de chaque source lumineuse. Si tous les rayons secondaires rencontrent une surface opaque, le point n’est pas éclairé par une source lumineuse mais seulement par la lumière ambiante. Par cette méthode, les faces cachées s’éliminent donc automatiquement. Il reste à tenir compte des cas particuliers (objet transparent, surface vitreuse, pas d’objet sur le trajet du rayon, réflexion sur une autre surface) et de la nature des sources de lumière.
Seules les sources de lumière connues pourront être prises en compte dans le calcul. Autrement dit, si l’objet est éclairé de façon indirecte, par exemple par réflexion de la lumière, ou même par diffusion à travers un autre objet, la méthode ne permet guère d’en tenir compte pour l’éclairement. En fait, les algorithmes peuvent être perfectionnés, en envoyant, par exemple, des rayons un peu au hasard pour savoir si l’on ne trouverait pas quelque part une source de lumière de ce type.
L’idée de départ se veut donc assez simplificatrice, mais l’expérience
prouve que, pour des scènes pas trop complexes et ne faisant intervenir que peu de sources lumineuses,
elle permet d’obtenir des images de synthèse étonnamment réalistes. Cette simplification
s’accommode de quelques autres algorithmes. Pour créer une image réaliste, II ne
suffit pas de mettre un observateur, une lumière, des objets et d’éliminer les faces
cachées. II faut aussi tenir compte des ombres portées par la lumière, des effets de texture
des matériaux à représenter, des couleurs, des réflexions et transparences, etc. Un
schéma résume les problèmes rencontrés pour obtenir les animations du programme
élémentaire de lancer de rayons.
POV est un programme de lancer de rayon disponible sous licence GPL, dont le fonctionnement peut paraître de premier abord un difficile à utiliser, mais qui se révèle à l'usage très efficace et très pédagogique. La version utilisée est la version 3.1g pour Windows.
t
Il permet d'acquérir les notions élémentaires de géométrie dans l'espace, les notions d'optique, ainsi qu'une pratique du raisonnement pour un usage artistique.
Notre but pour cette première expérience est la modélisation d’une boule de chrome reflétant un sol à damier rouge et bleu.
Voici le programme :
#include "colors.inc"
#include "metals.inc"
camera {location <0,5,-10> look_at <0,0,0>}
light_source {<2,4,-3> color White}
sphere {<0,0,0> 2.1 texture {T_Chrome_3E}}
plane {y,-2 pigment {checker colour Red colour Blue scale 2}}
Les deux premières lignes chargent les bibliothèques contenant la description des couleurs et des métaux.
La troisième ligne indique d'où la scène est observée (camera location) et vers quel point l'observateur fixe son regard (camera look_at).
La quatrième ligne précise l'éclairage de la scène (éclairage à symétrie sphérique et lumière blanche)
La cinquième ligne fait dessiner une sphère en chrome.
La sixième ligne fait dessiner le sol en damier rouge et bleu.
Voici le résultat :

La scène est ainsi décrite uniquement à partir d'objets géométriques ainsi que des objets décrits définis mathématiquement. On peut ainsi concevoir des scènes bien plus complexes.

Mais le principe reste toujours le même.
Des notions de physique, principalement d'optique sont nécessaires pour représenter la scène (nature des matériaux, nature des sources d'éclairage...)
On peut ainsi, à partir de formes simples (comme par exemple des sphères) de réaliser des formes plus complexes grâce à des opérations comme l'union, la différence, l'intersection).
| Union |
L'union permet d’assembler deux (ou plus) formes pour n’en former plus qu’une seule.

| Intersection |
L'intersection permet de combiner deux (ou plus) formes pour en former une nouvelle constituée par l’aire commune occupée par toutes les formes de départ (seules les parties communes des objets sont visibles).

|
Différence |
La différence permet de soustraire le volume d’une forme à une autre.

Voici pour finir une scène composée uniquement de tores, ce permet de montrer ce qu'on peut réaliser en utilisant que une seule forme (le tore) :

Ray-tracing, Mustafa Sauna, Science et vie micro n°58, février
1989
La synthèse selon POV !, Denis Boder, Presqu'offert n°13, mai-jun 1987
Pov-Ray, Denis Boder, Prequ'offert n°31, mai-juin 2000
POV pour windows version 3.1g
POV pour DOS version 3.1g
Discuter du sujet dans le forum